Processingで描画することができるオブジェクトにはそれぞれ座標が存在します。Processingの実行ウィンドウの座標(グローバル座標)は常に左上が座標の原点になりますが、個々のオブジェクトの座標(ローカル座標)は移動、回転、伸縮することができます。
座標の移動
それでは、まず座標の移動について解説します。はじめに座標の移動を実行せずに図形を描画します。
void setup(){
size(400,400);
}
void draw(){
rect(0,0,50,50);
}このプログラムでは図形(正方形)の原点(図形の左上)をX座標=0,Y座標=0(以下(0,0)と記述)としているため、実行ウィンドウの左上から描画されています。
次に図形(正方形)のローカル座標をtranslate()関数を使って移動させてみましょう。
void setup(){
size(400,400);
}
void draw(){
translate(200,200);
rect(0,0,50,50);
}上のコードでは図形(正方形)の座標は(0,0)であるにも関わらず、実際に図形が描画される位置はtranslate()関数によって実行ウィンドウ上の(200,200)の位置に移動しています。
更に、複数のtranslate()関数を使った例を見てみましょう。
void setup(){
size(400,400);
}
void draw(){
background(0);
translate(mouseX,mouseY);
rect(0,0,50,50);
translate(50,50);
rect(0,0,25,25);
}上のコードでは、複数のtranslate()関数の効果が合成されることが確かめられます。
座標の回転
図形のローカル座標を回転させるためにはrotate()関数を使用します。rotate()関数のパラメータは1つだけで、回転角(ラジアン)を指定します。
それでは、図形の座標を回転させてみましょう。
void setup(){
size(160,160);
}
void draw(){
background(0);
rotate(mouseX/100.0);
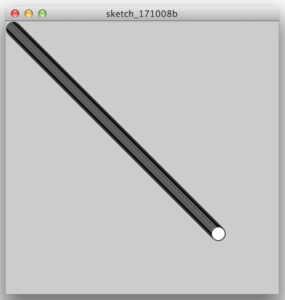
rect(0,0,160,20);
}上のコードではrotate()関数を使って図形を回転しています。回転角(ラジアン)は0〜360度までを0〜約6.28の数値で表します。このコードではX座標を100.0で割ることで回転角(ラジアン)に変換しています。
座標の伸縮
座標を伸縮させるには、scale()関数を使用します。scale(2)とすると画面内の図形はすべて2倍の大きさになります。scale(0.5)とすると、図形はすべて半分の大きさになります。
それでは、以下のコードで確認してみましょう。
void setup(){
size(400,400);
}
void draw(){
rect(0,0,100,100);
scale(0.5);
rect(0,200,100,100);
scale(4);
rect(0,100,100,100);
}座標の復元
座標系の変換(移動、回転、伸縮)は、変換後のすべてのコードに影響を及ぼしますが、その影響の範囲を限定し、変換以前の状態に復元することができます。pushMatrix()関数とpopMatrix()関数を使うことで変換した座標の復元ができます。pushMatrix()関数を実行すると、それ以降に記述した座標系変換の情報が記録され、popMatrix()が使われると変換前の座標系に戻ります。pushMatrix()関数とpopMatrix()関数は常にペアで使う必要があります。
それでは、以下のコードを使って確認してみましょう。
void setup(){
size(400,400);
}
void draw(){
background(0);
pushMatrix();
translate(mouseX,mouseY);
ellipse(0,0,50,50);
popMatrix();
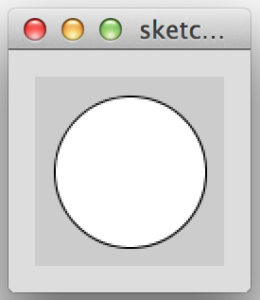
ellipse(200,200,200,200);
}上のコードでは1つめの図形(円)の座標系の移動をマウスの座標に合わせていますが、pushMatrix()関数とpopMatrix()関数を使って、座標系の移動が復元されるため、2つめの円は座標系の移動の影響を受けません。
練習課題07: 以下の条件を全て満たす作品を作成してください。 ・固定された座標を持つ図形が表示されていること。 ・マウスの動きによって変化する図形が表示されること。 ・マウスの動きによって色(背景色や図形の色)が変化すること。