学習教材・研究資料

ピクセル（情報の単位）
コンピューターで画像を扱う際の色情報（色相・彩度・明度）を持つ最小単位。コンピューターで扱われる画像のサイズは縦横のピクセル数で表される。
例）640ピクセル x 480ピクセルの画像を作成する。

ドット（物理的な単位）
物理的な画像出力装置であるモニター（ディスプレイとも呼ぶ）やプリンターで表現できる最小単位。
例）フルHD画質のモニターの画素は1920ドット×1080ドット

DPI (dots per inch)
モニターやプリンターにおいて1インチ（1平方インチではない）の幅の中にどれだけのドットを表現できるかを表す単位。従来、モニターでは72dpiの解像度が標準であったが現在ではより高解像度のモニターが製造されている。印刷物の解像度は300dpi以上が必要となる。低解像度のデータを印刷すると不鮮明になる。
例）350dpiの写真画像データを印刷会社に入稿する。

ファイルサイズへの影響
デジタルデータは、そのデータが持っている情報量によって容量が異なる。デジタルデータの容量はバイト (byte)という単位で表される。画像データでは作成されたデータ（ファイル）の解像度が容量の大小に関わってくる。詳細で鮮明な画像を作成すると高解像度になるが、データ容量が不必要に大きすぎるとソフトの動作が重たくなったり、完成したデータをメールで送れなくなったりする。
例）画像ファイルを作成したら容量が100MB(メガバイト）になってメールで送れなかった。

⚫︎ポイント
不適切な解像度のデータ作成は現場では許容されません。不必要に大容量のデータをメールで送れば長時間のダウンロードを相手に強いることになり、場合によっては送ることができません。また、印刷するポスターやハイビジョン画質などのデータを要求されているのに低解像度のデータでは使用することができません。

画像をコンピューターで取り扱うためにはデジタルデータ化する必要がある。デジタルデータ化するための方式はいくつか存在する。それぞれの方式は画像フォーマットと呼ばれる。以下に代表的な静止画の画像フォーマットを記載する。

RAW（ロウ）
デジタルカメラなどで撮影されたままの状態の未加工な画像データのこと。データ容量が大きく、カメラメーカーごとにデータ化の方法が異なる（標準化されていない）。

主要な画像フォーマット：

JPEG（ジェイペグ）
画像を圧縮して記録する方式。基本的に非可逆圧縮という一度圧縮したら元の状態には戻せない方式である。写真など階調の変化が多い画像を小さい容量で記録することに向いており、よく使われている方式。 JPGとも表記する。

GIF（ジフ）
256色以下の画像を扱うことができる画像形式。可逆圧縮形式を採用しており、圧縮された画像を元の状態に戻すことができる。階調の少ない画像の圧縮に向いているため、イラストやロゴ、アイコンなど写真以外の画像記録に向いている。GIFアニメーション形式で保存することでアニメーションとして記録できる。WEBページなどでよく使われている。

PNG（ピーエヌジー）
GIFと違って256色以下の制限が無い可逆圧縮形式の画像形式。上述したGIFが特許問題で論争を起こしている際に代替技術として開発が進められた（現在では特許の有効期限が切れたのでGIFは自由に使用できる）。透明色の表現はGIFよりも優れている。

TIFF（ティフ）
画像データを解像度や色情報などが異なる様々な形式で記録できるため、アプリケーションソフトに依存することがあまり無いフォーマット。

その他注意すべき項目：

PSD（ピーエスディー）
Adobe Photoshopで主に利用されるファイル形式。Photoshop Dataを略したもの。画像ファイルとは異なり、Photoshop上のレイヤーやパスなどの情報も記録されている。Adobe PhotoshopやAdobe製品でしか扱えないことが多いので注意。

カラーモードについて
Processingで色を表現するためにはカラーモデルを使って色を指定する必要があります。Processingで用いられるカラーモデルにはRGBモデルとHSBモデルがあります。

RGBモデルは、Red (赤)、Green (緑)、Blue (青) の三つの原色を混ぜて色を再現する加法混合の一種です。

HSBモデルはHue（色相）、Saturation（彩度）、Brightness（明度）の三つの成分から色を再現する方法です。

Processingでは、カラーモードを指定することで、RGBモデルとHSBモデルのいずれのカラーモデルを選ぶことができます。カラーモードは、以下のように設定します。

colorMode(mode, range1, range2, range3, range4);

mode 　RGBまたはHSB
range 　色を指定する値の範囲(intまたはfloat):省略可
range1 赤または色相の範囲(intまたはfloat):省略可
range2 緑または彩度の範囲(intまたはfloat):省略可
range3 青または明度の範囲(intまたはfloat):省略可
range4 透明度の範囲(intまたはfloat) :省略可

ProcessingのデフォルトのカラーモデルはRGBモデルになるため、RGBモデルで各色256段階の範囲で指定する場合は特にcolorMode()関数を使用する必要はありません。

色の設定について
Processingでは、背景の色、図形の線の色、図形の面の色をそれぞれ設定することができます。色を設定するための関数を以下に記載します。

背景の色
background(R,G,B);

線の色
stroke(R,G,B);

面の色
fill(R,G,B);

上記の関数のR,G,Bは色を表すパラメータで、R(Red:赤)、G(Green:緑)、B(Blue:青) の三つの原色を表しており、それぞれ0〜255までの数値で色を指定します。
0は色の最小値でそれぞれの色の成分が表示されません。255は色の最大値となります。

例：R, G, Bが0, 0, 0なら黒、255,0,0なら赤、255,255,255なら白

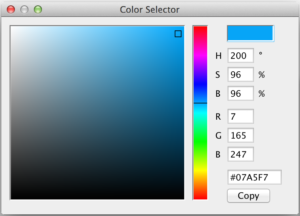
Processingでは色の選択に使えるツールが備わっています。メニューからTools>Color Selectorを選んで下記のウィンドウを表示し、カラーパレットから色を選択すると、RGB, HSBそれぞれの色の数値やカラーコードが表示されるので、この数値を参考にコード上の数値を記述します。

背景の色を設定する
背景の色を設定してみましょう。背景の色を設定するには、background()関数を使用します。

background(255,0,0);

*background()関数をsetup()関数内で使用するか、draw()関数内で使用するかによって完成するアプリケーションの動作に違いが生じるので注意が必要です。

線の色を設定する
基本図形の線の色を設定してみましょう。線の色を設定するにはstroke()関数を使用します。
また、線を描画しない場合にはnoStroke()関数を使用します。

size(400,400);
background(0);
stroke(255,0,0);
ellipse(100,200,100,100);
noStroke();
ellipse(300,200,100,100);

面の色を設定する
基本図形の面の色を設定してみましょう。面の色を設定するにはfill()関数を使用します。
また、面を描画しない場合にはnoFill()関数を使用します。

size(400,400);
background(255);
fill(255,0,0);
ellipse(150,200,300,300);
noFill();
ellipse(250,200,300,300);

透明度を設定する
図形の面の色や線の色を指定するstroke()関数やfill()関数に、透明度を設定する四つ目のパラメータを加えることで図形の透明度を設定できます。このパラメータをアルファ値と呼びます。

線の透明度設定：
stroke(R,G,B,alpha);

面の透明度設定：
fill(R,G,B,alpha);

アルファ値の値の範囲は0から255で、0にすると完全に透明になり（表示されない）、255にすると完全に不透明になります（アルファ値を指定しない場合と同じ）。
1から254までの値の範囲では半透明になり、下の色と混ざり合った透けた色が表現できます。

size(400,400);
background(255);
stroke(255,0,0,125);
fill(7,165,247,200);
ellipse(150,200,300,300);
stroke(0,255,0,100);
fill(247,7,216,200);
ellipse(250,200,300,300);

練習課題04-05：基本図形と色の設定を使用してグラフィック作品を作成してください。
作品には英数でタイトルをつけてください。
画面サイズは幅400ピクセル、高さ400ピクセルとします。

Processingには、あらかじめ基本的な図形を描く関数が用意されています。以下に基本的な図形の描画方法を記載します。

点
point(x座標, y座標);

線
２つの座標(x座標1, y座標1)と(x座標2, y座標2)を結ぶ１本の直線を描きます。
line(x座標1, y座標1, x座標2, y座標2);

方形
方形（正方形や長方形）は、４つのパラメータで設定します。方形の左上の角を基準点にx座標, y座標で指定し、幅と高さを指定します。
rect(x座標, y座標, 幅, 高さ);

円形
円形（正円や楕円）は、４つのパラメータで設定します。円形の中心を基準点にx座標, y座標で指定し、幅と高さを指定します。
ellipse(x座標, y座標, 幅, 高さ);

三角形
三角形は６つのパラメータを指定して描きます。
triangle(x座標1, y座標1, x座標2, y座標2, x座標3, y座標3);

四辺形
四辺形は８つのパラメータを指定して描きます。
quad(x座標1, y座標1, x座標2, y座標2, x座標3, y座標3, x座標4, y座標4);

描線の太さ
図形の描線の太さを変更できます。描線のデフォルトは1ピクセルですが、strokeWeight()関数を使って変更できます。strokeWeight()関数のパラメータは１つで、太さをピクセル数で指定します。
以下のように記述します。

size(400,400);
strokeWeight(8);
ellipse(200,200,200,200);

描画の順序
プログラムはコードの先頭１行目から順に読み込まれていくため、コードを書く順番は図形の重なり順などに大きく影響します。
重なり合う複数の図形がある場合は、最後に描かれた図形が一番上に重なって表示されます。

描画モード
図形を描画する際に、描画の基準点を設定することができます。
方形の記述ではrectMode()関数を使用して以下のように基準点を設定できます。

rectMode(CORNER) rect(左上頂点のx座標, 左上頂点のy座標, 幅, 高さ);　//デフォルトではこの基準点を使う
rectMode(CORNERS) rect(左上頂点のx座標, 左上頂点のy座標, 右下頂点のx座標, 右下頂点のy座標);
rectMode(CENTER) rect(中心のx座標, 中心のy座標, 幅, 高さ);
rectMode(RADIUS) rect(中心のx座標, 中心のy座標, 幅の半分, 高さの半分);

円形の記述ではellipseMode()関数を使用して以下のように基準点を設定できます。

ellipseMode(CENTER) ellipse(中心のx座標, 中心のy座標, 幅（直径）, 高さ（直径）); //デフォルトではこの基準点を使う
ellipseMode(RADIUS) ellipse(中心のx座標, 中心のy座標, 幅（半径）, 高さ（半径）);
ellipseMode(CORNER) ellipse(円が収まる四角い領域の左上角のx座標, 円が収まる四角い領域の左上角のy座標, 幅（直径）, 高さ（直径）);
ellipseMode(CORNERS) ellipse(円が収まる四角い領域の左上角のx座標, 円が収まる四角い領域の左上角のy座標, 円が収まる四角い領域の右下角のx座標, 円が収まる四角い領域の右下角のy座標);

コードは以下のように記述します。

size(400,400);
rect(100,50,80,80);
ellipse(100,50,80,80);
ellipseMode(CORNER);
rect(200,50,80,80);
ellipse(200, 50, 80, 80);

画面サイズの設定
Processingでは、画面（実行ウィンドウ）のサイズを以下の関数*を使用して設定することができます。

size(画面の幅, 画面の高さ);

*関数とはプログラミングの構成単位であり、パラメータと呼ばれる数値などで定義することができます。

それでは、幅800ピクセル*、高さ600ピクセル*のウィンドウを以下のようにテキストエディタに記述して作成してみましょう。

size(800,600);

*パラメータで扱う単位はコンピュータの画面上で画像を扱う際の最小単位であるピクセル（Pixcel）です。

練習課題　数値を変えて様々なサイズの画面（実行ウィンドウ）を作成してみよう。

座標について
座標とは空間上の１点を指定するための方法です。画面に図形を描くためには、図形の位置を決める必要があり、座標を利用します。Processingの画面（実行ウィンドウ）では以下のようにして画面上の１点を指定します。

画面の左上を基準点とし右に移動した距離xと下に移動した距離yで１点を指定する。

それでは、サイズが幅400ピクセル、高さ４００ピクセルの画面（実行ウィンドウ）を作成し、x座標が200ピクセル、y座標が200ピクセルの位置に点を描画してみましょう。

点の描画にはpoint()関数を用います。
point(x座標,y座標);

size(400,400);
point(200,200);

練習課題03:　幅400ピクセル、高さ400ピクセルの画面（実行ウィンドウ）の四隅に点を描画してみよう。

Processingでサウンドデータを扱う際に使われるサウンドライブラリminimを使ってみましょう。

minimの解説ページ（英語）

サウンドファイルの再生
はじめに、サウンドファイルを再生するコードを作成してみましょう。
再生するサウンドファイルはmp3形式とします。フリー素材などをダウンロードしてファイル名をsound.mp3としましょう。
SketchメニューからAdd File…メニューを選択しsound.mp3をdataフォルダに読み込んでおきます。
それでは以下のコードを記述してみましょう。

import ddf.minim.*;
 
Minim minim;
AudioPlayer sound;
 
void setup(){
  size(400, 400);
  minim = new Minim(this);
  sound = minim.loadFile("sound.mp3");
  sound.play();
}
 
void draw(){
  background(0);
}
 
void stop(){
  sound.close();
  minim.stop();
  super.stop();
}

このコードではimport ddf.minim.*;の行でサウンドライブラリminimを呼び出しています。Minim型変数のminimを宣言し、AudioPlayer でサウンドファイルを格納する変数soundを宣言します。sound = minim.loadFile(“sound.mp3”);の行でサウンドファイルsound.mp3を読み込み、sound.play();でサウンドファイルを再生しています。またプログラム終了時にサウンドファイルの再生を止めるため、void stop(){ 〜 }を記述しておきます。

サウンドファイルの巻き戻し
サウンドファイルを巻き戻すことで再生したサウンドファイルを何度も再生することができます。以下のコードを記述してみましょう。

import ddf.minim.*;
 
Minim minim;
AudioPlayer sound;
 
void setup()
{
  size(400, 400);
  minim = new Minim(this);
  sound = minim.loadFile("sound.mp3");
  fill(0, 255, 0);
}
 
void draw()
{
  background(255);
}
 
void stop()
{
  sound.close();
  minim.stop();
  super.stop();
}
 
void mousePressed() { 
    sound.play();
    sound.rewind();
}

このコードではsound.play();の行でサウンドファイルを再生した後に、sound.rewind();でサウンドファイルを巻き戻すことでマウスを画面上でクリックするごとにサウンドファイルを無限に再生させています。

ミリ秒
Processingでは時間の経過をプログラムで扱うことができます。まずはじめにmillis()関数を使ってみましょう。millis()関数はプログラムが起動してからの経過時間をカウントしています。単位はミリ秒（千分の１秒）です。（1000ミリ秒で１秒）
それでは以下のコードを記述してみましょう。

void setup(){
  size(400,400);
}

void draw(){
  background(255);
  int timer = millis();
  translate(200,200);
  rotate(timer/1000.0);
  line(0,0,100,100);
}

秒、分、時
Processingではシステム（コンピュータのOS）に設定された時刻を取得することができます。
秒の取得は second()関数、分の取得は minute()関数、時の取得は hour()関数を使用します。
はじめに、second()関数を使ったコードを作成してみましょう。

void setup() {
  size(600,200);
  frameRate(60);
}

void draw() {
  background(255);
  int s = second();
  int time = s*10;
  line(time,0,time,400);
}

上のコードでは線のX座標をsecond()関数に対応させています。

それでは、second()関数に加えて、minute()関数とhour()関数を使ったコードを記述してみましょう。

void setup() {
  size(600,200);
  frameRate(60);
}

void draw() {
  background(255);
  int s = second()*10;
  int m = minute()*50;
  int h = hour()*50;
  for(int i=0;i<600;i+=50){
    line(i,0,i,200);
  }
  ellipse(s,50,20,20);
  ellipse(m,100,20,20);
  ellipse(h,150,20,20);
}

上のコードは、second()関数、minute()関数、hour()関数を使って、図形（円）で秒、分、時を表現しています。

Processingで描画することができるオブジェクトにはそれぞれ座標が存在します。Processingの実行ウィンドウの座標（グローバル座標）は常に左上が座標の原点になりますが、個々のオブジェクトの座標（ローカル座標）は移動、回転、伸縮することができます。

座標の移動
それでは、まず座標の移動について解説します。はじめに座標の移動を実行せずに図形を描画します。

void setup(){
  size(400,400);
}

void draw(){
  rect(0,0,50,50);
}

このプログラムでは図形（正方形）の原点（図形の左上）をX座標=0,Y座標=0（以下(0,0)と記述）としているため、実行ウィンドウの左上から描画されています。

次に図形（正方形）のローカル座標をtranslate()関数を使って移動させてみましょう。

void setup(){
  size(400,400);
}

void draw(){
  translate(200,200);
  rect(0,0,50,50);
}

上のコードでは図形（正方形）の座標は(0,0)であるにも関わらず、実際に図形が描画される位置はtranslate()関数によって実行ウィンドウ上の(200,200)の位置に移動しています。

更に、複数のtranslate()関数を使った例を見てみましょう。

void setup(){
  size(400,400);
}

void draw(){
  background(0);
  translate(mouseX,mouseY);
  rect(0,0,50,50);
  translate(50,50);
  rect(0,0,25,25);
}

上のコードでは、複数のtranslate()関数の効果が合成されることが確かめられます。

座標の回転
図形のローカル座標を回転させるためにはrotate()関数を使用します。rotate()関数のパラメータは１つだけで、回転角（ラジアン）を指定します。
それでは、図形の座標を回転させてみましょう。

void setup(){
  size(160,160);
}

void draw(){
  background(0);
  rotate(mouseX/100.0);
  rect(0,0,160,20);
}

上のコードではrotate()関数を使って図形を回転しています。回転角（ラジアン）は０〜３６０度までを0〜約6.28の数値で表します。このコードではX座標を100.0で割ることで回転角（ラジアン）に変換しています。

座標の伸縮
座標を伸縮させるには、scale()関数を使用します。scale(2)とすると画面内の図形はすべて２倍の大きさになります。scale(0.5)とすると、図形はすべて半分の大きさになります。
それでは、以下のコードで確認してみましょう。

void setup(){
  size(400,400);
}

void draw(){
  rect(0,0,100,100);
  scale(0.5);
  rect(0,200,100,100);
  scale(4);
  rect(0,100,100,100);
}

座標の復元
座標系の変換（移動、回転、伸縮）は、変換後のすべてのコードに影響を及ぼしますが、その影響の範囲を限定し、変換以前の状態に復元することができます。pushMatrix()関数とpopMatrix()関数を使うことで変換した座標の復元ができます。pushMatrix()関数を実行すると、それ以降に記述した座標系変換の情報が記録され、popMatrix()が使われると変換前の座標系に戻ります。pushMatrix()関数とpopMatrix()関数は常にペアで使う必要があります。
それでは、以下のコードを使って確認してみましょう。

void setup(){
  size(400,400);
}

void draw(){
  background(0);
  pushMatrix();
  translate(mouseX,mouseY);
  ellipse(0,0,50,50);
  popMatrix();
  ellipse(200,200,200,200);
}

上のコードでは１つめの図形（円）の座標系の移動をマウスの座標に合わせていますが、pushMatrix()関数とpopMatrix()関数を使って、座標系の移動が復元されるため、２つめの円は座標系の移動の影響を受けません。